-
1. 匿名 2017/04/03(月) 17:32:27
浜松市立神久呂小学校を今春卒業した山本賢一朗君。小5の時、分数に苦手意識を感じたという。友人も悩んでいた。掛けるのになぜ、答えは小さくなるのか。割り算ではなぜ、割る方の分母と分子を入れ替えて逆数にするのか……。
学習塾の経営に携わる父裕一朗さん(40)にも疑問をぶつけ、やがてものさしで分数を考える発想にたどり着く。1とその数以外では割り切れない「素数」の目盛りだけがついた京都大の「素数ものさし」がヒントになった。
+122
-8
-
2. 匿名 2017/04/03(月) 17:33:33
天才だ!!+235
-11
-
3. 匿名 2017/04/03(月) 17:34:55
ごめん、全然分かんない+879
-16
-
4. 匿名 2017/04/03(月) 17:35:03
もう私には何の事やら全く理解出来んけど、凄いね!+466
-4
-
5. 匿名 2017/04/03(月) 17:35:08
分数が苦手が故の才能開花!!
素晴らしい!!+194
-4
-
6. 匿名 2017/04/03(月) 17:35:16
何言ってんのかさっぱり分からん
普通に覚えた方が早そう+393
-14
-
7. 匿名 2017/04/03(月) 17:35:37
頭いいなぁ+37
-2
-
8. 匿名 2017/04/03(月) 17:35:42
”これはそういうもの”で覚えるだけで終わるんじゃなく
ちゃんと理解しようとするのが凄いね
学者肌だ+317
-5
-
9. 匿名 2017/04/03(月) 17:36:00
レゴで考えるのもわかりやすいよ
+508
-11
-
10. 匿名 2017/04/03(月) 17:36:13 ID:capMI1JNaG
しっかりしてる、偉くなりそう+59
-2
-
11. 匿名 2017/04/03(月) 17:36:16
この定規の範囲であれば暗算できるのよ+94
-3
-
12. 匿名 2017/04/03(月) 17:36:51
これは深く考えたら負けだと思って、言われた通りひっくり返してかけ算してた。
大丈夫。その時期過ぎたら一生使わないから。+266
-6
-
13. 匿名 2017/04/03(月) 17:37:01
疑問を感じる時点で頭良いんだろうな+130
-3
-
14. 匿名 2017/04/03(月) 17:37:13
いまいちわからんw
賢いがるちゃん民解説よろ+58
-4
-
15. 匿名 2017/04/03(月) 17:37:21
>>9確かに視覚的でわかりやすいけど、これは足し算引き算だけだね+50
-3
-
16. 匿名 2017/04/03(月) 17:37:25
算数が苦手なんじゃなくて
計算方法に理論が追いつかなくて分からないってタイプの子だったんですね。
天才の卵かぁ
+178
-2
-
17. 匿名 2017/04/03(月) 17:37:31
もはや分数の計算ができない私・・・+72
-4
-
18. 匿名 2017/04/03(月) 17:37:56
逆にわからなくなった・・・。+102
-3
-
19. 匿名 2017/04/03(月) 17:38:02
小学生の頃なんて何にも考えてなかったわ+26
-1
-
20. 匿名 2017/04/03(月) 17:39:08
よく理解出来ないけど、この子は頭がいいんだろうなってのは分かる☆+31
-2
-
21. 匿名 2017/04/03(月) 17:39:19
図見たけどよくわかんなかった+22
-4
-
22. 匿名 2017/04/03(月) 17:39:45
+78
-2
-
23. 匿名 2017/04/03(月) 17:40:28
物を2つに割ってこれが二分の一ね!と言われた方が早いと思う
これが分からんなら語学力とかに問題があるとしか思えない+10
-14
-
24. 匿名 2017/04/03(月) 17:41:19
理解しようと何度もものさし見たけど、
はぁ?
ってなる。+61
-9
-
25. 匿名 2017/04/03(月) 17:42:28
分数って苦手な子はほんと苦手だったよね
スッと理解できる子は
こんなの見たら逆に分かりづらいわ!って言いそう+20
-2
-
26. 匿名 2017/04/03(月) 17:45:02
アップデートできない脳みそだから全然わからない+12
-6
-
27. 匿名 2017/04/03(月) 17:45:11
発案て書いてあるけど、これよくある説明の仕方だよ。
こだわってしっかり考えたのはえらいと思うけどさ。+19
-1
-
28. 匿名 2017/04/03(月) 17:45:15
+44
-4
-
29. 匿名 2017/04/03(月) 17:45:33
分数が分からない子は足算引算に固定観念を強く持ちすぎるからだと思う
何で割算なのに掛け算しなきゃいけないの?って思うタイプ
+7
-1
-
30. 匿名 2017/04/03(月) 17:46:13
分数の割り算でひっくり返すのは
割る方の数を1にしてしまおうという事だからだよ。
割られる方にも同じ数をかけるの。
+24
-3
-
31. 匿名 2017/04/03(月) 17:46:36
とりあえず分数ものさしとレゴの画像保存させてもらった+13
-0
-
32. 匿名 2017/04/03(月) 17:48:12
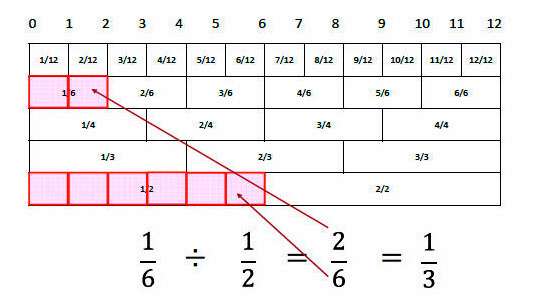
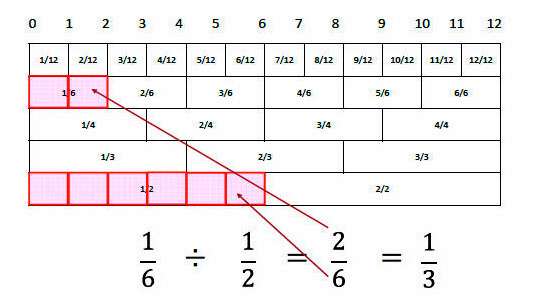
12分の1を「1」として
6分の1(12分の1が「2つ」)÷2分の1(12分の1が「6つ」)で、この「2つ」÷「6つ」って計算に変換しようってことかな?
・・・自分で説明してても分かりにくいんだけど算数苦手な子にこれわかるのかな+9
-2
-
33. 匿名 2017/04/03(月) 17:50:20
わかんなーい。
でも、分数の計算に関しては出来なくても40歳すぎた今まで困ったことないからいいや。+20
-5
-
34. 匿名 2017/04/03(月) 17:50:22
わかりやすい!+5
-1
-
35. 匿名 2017/04/03(月) 17:51:37
>>9
つまり1が何なのかを示せば分かりやすいって事ね+3
-0
-
36. 匿名 2017/04/03(月) 17:51:41
上の目盛りが分子、したの目盛りが分母になるよーとしか教えられなそう。理屈を理解できるのかはまた別だね+0
-0
-
37. 匿名 2017/04/03(月) 17:52:32
この説明見てやっと意図するところがわかった![「分数ものさし」小学生が発案 計算法、目盛りで理解-静岡大、教材化に向け研究]()
+16
-3
-
38. 匿名 2017/04/03(月) 17:53:49
>>9
5分の1は?+2
-1
-
39. 匿名 2017/04/03(月) 17:53:55
>>37だけどモノサシの意図はわかったけど、それと割り算が結びつかなくない?
割り算としての説明の仕方が難しい。+37
-2
-
40. 匿名 2017/04/03(月) 17:54:27
基本的な読み書きや計算はともかく、大半は大人になって実生活で使うことないよね。
+3
-0
-
41. 匿名 2017/04/03(月) 17:54:33
小学生の頃意味分からない意味分からない言っていたら意味なんて考えないで覚えるの!って言われたな(苦笑)+5
-0
-
42. 匿名 2017/04/03(月) 17:55:28
>>32
それで合ってると思う。リンク先の記事の解説を読んだら
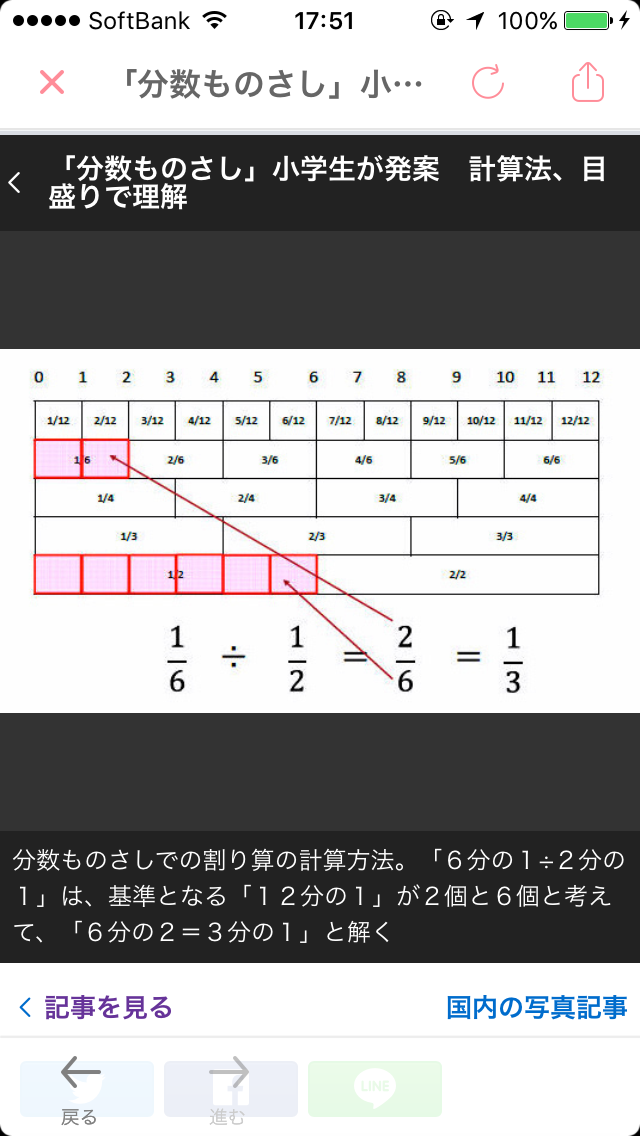
「分数ものさしでの割り算の計算方法。
「6分の1÷2分の1」は、基準となる「12分の1」が2個と6個と考えて、
「6分の2=3分の1」と解く 」
と書いてあったからね。
でも、私が小学生だったら、その説明でも絶対わからないだろうな。+17
-0
-
43. 匿名 2017/04/03(月) 17:59:48
結局このモノサシも「こういうものだと覚えろ」って感じで詳しい説明には向かないなぁ+30
-0
-
44. 匿名 2017/04/03(月) 18:00:00
>>9
レゴの方がめっちゃ分かりやすい!+50
-0
-
45. 匿名 2017/04/03(月) 18:02:38
ちょっと少年、君は天才
飛び級で大学まで行けそう+2
-4
-
46. 匿名 2017/04/03(月) 18:03:26
お名前の通り、賢い子だね+3
-2
-
47. 匿名 2017/04/03(月) 18:03:29
レゴが凄い❗+18
-0
-
48. 匿名 2017/04/03(月) 18:03:57
今更?!これ前からあるよ... まさか発明とか思ってる?+3
-0
-
49. 匿名 2017/04/03(月) 18:05:42
早く特許と商標申請するんだよー
人間のゴミクズ野郎に持ってかれちゃうよー+3
-4
-
50. 匿名 2017/04/03(月) 18:07:11
私ダメだ。
1/6 ÷ 1/2
= 1/6 ÷ 3/6
= 1/3
という数字の並びに置き換えてやっとうっすら理解できる。
小学生の時のIQ160あったんだけど。+3
-1
-
51. 匿名 2017/04/03(月) 18:08:10
>>49 いやいや、既存証明できるから+0
-0
-
52. 匿名 2017/04/03(月) 18:09:36
ツイッターだかでも「1+1=2」の計算式で、なぜこの計算式もこのこと似たように理解できない人いたよね+0
-2
-
53. 匿名 2017/04/03(月) 18:09:37
>>9
数字と色の組み合わせを統一して(; ;)
+2
-0
-
54. 匿名 2017/04/03(月) 18:10:56
>>52
すみません、日本語でお願いします。+0
-0
-
55. 匿名 2017/04/03(月) 18:28:30
>>17
やばい+2
-0
-
56. 匿名 2017/04/03(月) 18:43:47
>>52
例えば粘土の塊と塊をくっ付けると1になるとかってやつかな?+0
-1
-
57. 匿名 2017/04/03(月) 19:01:10
読んでたら眠くなってきた…
+2
-0
-
58. 匿名 2017/04/03(月) 19:05:47
>>30
そういえば習った!
ありがとう(*^^*)+0
-0
-
59. 匿名 2017/04/03(月) 19:07:30
余計難しいわw!
余計な疑問は持たずに、ひっくり返して計算した方がラク。
まあ、本当に理解しているとは言わないんだろうけど。。+7
-0
-
60. 匿名 2017/04/03(月) 19:20:55
分数の足し算と引き算はまぁわかる
でも掛け算と割り算がなぁ
割り算て、例えば「9個のみかんを3人で分けたら、一人いくつずつになるでしょうか?」みたいな学び方をしたから
「9を1/3で割る」とかの概念がまったく理解できない
1/3で割るって何
+13
-0
-
61. 匿名 2017/04/03(月) 19:22:47
>>42
40代だけど全然分からん・・・・
昔からほんとうに算数はダメだったけど、思い起こせばここでつまずいてると思う。+2
-0
-
62. 匿名 2017/04/03(月) 19:49:26
まっったく分からない!+0
-0
-
63. 匿名 2017/04/03(月) 20:11:57
>>60
普段使っている数字は分母の1が隠されていて、例えば例題では3人と書いてあるけど、分数にすると3/1になるんだよ。9÷3は9÷3/1となり掛け算として9×1/3と表される。9/3は約分して3/1、分母の1を省略して3となる。
これを次の「9を1/3で割る」で当てはめると、9÷1/3は掛け算にすると9×3/1となるので27/1となり分母が省略されて27となる。
ってことらしい。+10
-0
-
64. 匿名 2017/04/03(月) 20:17:07
+7
-0
-
65. 匿名 2017/04/03(月) 20:28:20
分数計算がひっくり返る理由なら、1÷2で考えればいいんだよ。
1つのパンを2つに分けた時、2分の1になるけど、2個にはならない。+3
-0
-
66. 匿名 2017/04/03(月) 20:36:16
思考回路ショートシマシタ+2
-0
-
67. 匿名 2017/04/03(月) 20:37:41
>>60
「9を1/3で割る」とかの概念がまったく理解できない
↑
9枚のピザを全部1/3切れにすると27人に配れるよね?
だから答えは27+16
-0
-
68. 匿名 2017/04/03(月) 21:03:50
掛ければ小さくなるんだよ。
細かいことは気にするな!
素直に計算だけすればいい+2
-0
-
69. 匿名 2017/04/03(月) 21:07:53
偉いね!理解できなくても解けたらいいって思うのがまあ普通だからね。逃げでもあるし。
この子は苦手を克服し、さらに上の段階にいけたね!素晴らしい!!+1
-0
-
70. 匿名 2017/04/03(月) 21:31:19
>>30 さん
24ですが、30さんのコメント見て、
なるほど!!ってなりました!
ありがとうございます!
+4
-0
-
71. 匿名 2017/04/03(月) 21:55:34
>>64
それだと
1/2÷3=1/6
1/6×3=1/2
になりそうだよ。
もう混乱してきたw+0
-1
-
72. 匿名 2017/04/03(月) 22:20:25
ひとつの物をふたりで分けると半分になるよね?
1÷2=1/2
ひとつのものを、ひとりにもらうと、ひとつ。
1÷1=1
ひとつの物を1/2人、つまり、ひとりの半分で分けると…
右手にひとつ、左手にひとつ…みたいな感じで、ふたつもらえる。
1÷1/2=2
どうしても、わからないなら、小数で考えたら?
1÷0.5=2
1÷1/2=2と同じだよね?
+7
-0
-
73. 匿名 2017/04/03(月) 22:53:17
>>72
文系は「1/2人」「ひとりの半分」の所で「!?」となって止まってしまうのです。+6
-0
-
74. 匿名 2017/04/04(火) 00:08:44
>>73
それです!そうです!!
現実離れした設定に思えて、
そこから先の話に入り込めないです、私も。
そーいうルールをみんななぜすんなり理解出来るのか不思議でなりませんでした(^-^;)+3
-0
-
75. 匿名 2017/04/04(火) 00:15:43
このやり方が身に付くと確実に逆効果
高校とか大学で絶対苦労する+7
-0
-
76. 匿名 2017/04/04(火) 03:12:04
え、これ頭の中で普通に考える事じゃない?
私は小学生の頃頭の中で似たような感じに考えてたけど+0
-0
-
77. 匿名 2017/04/04(火) 04:25:12
>>71
計算しちゃうからですよ笑
太い赤枠どおしを見て、あ〜3倍の大きさだなぁ〜と思うだけです。
私が超面倒くさがりで計算しなさ過ぎなのかな笑+0
-0
-
78. 匿名 2017/04/04(火) 05:37:48
>>73
>>74
【文系の方向け】
割り算は…
10÷2 とは、
「10を2つに割るといくつ?」
の他に
「10の中に2はいくつある?」
と同じ意味です。
そうすると>>60さんの
「9を1/3で割る」
の場合
9÷1/3とは、
「9の中に1/3はいくつある?」
と同じ意味ですので、ピザにたとえると、
『1/3切れとは1枚のピザを3つに分けた物。
それが9枚分あるから全部で27切れできる。
つまり、
" 9枚のピザの中には1/3切れが27個ある"
といえる。
従って、答えは27』
と文系の方も(笑)答えを導き出す事ができます。+4
-0
-
79. 匿名 2017/04/04(火) 06:56:44
>>78さん
74です。
割り算の説明ありがとうございます‼
割るってことは、
いくつあるか
という見方もできるのですね。
子供の頃に誰かに言ってもらえたらもう少し楽しい算数の時間を過ごせていたはずです(TдT)
速さ=距離÷時間
と教わった時の衝撃も未だに忘れられません…。
色々な長さになる距離を、
時計でしか計れない時間で割るなんて壮大な世界、
受け入れるだけで当時の自分にはイッパイイッパイでした(^-^;)+3
-0
-
80. 匿名 2017/04/04(火) 07:58:48
>>79
速さ=距離÷時間
「1時間で何㎞進んだのか?」
と距離で速さを表現してるから
○㎞/h という「距離」を書くのか。
みたいに考えてました。
(考えてないですねこれじゃ笑)+1
-0
-
81. 匿名 2017/04/04(火) 08:17:06
>>80さん
コメントありがとうございます‼
79です。
速さ=距離÷時間
「1時間で何㎞進んだのか?」
⬆ここは理解出来ます。
と距離で速さを表現してるから
⬆距離で速さを表現で脱落しました(T^T)
いつもそうで、教えてくれる人は「は?」となる方がほとんどでした。
○㎞/h という「距離」を書くのか。
⬆一時間で何キロ進んだかの表記ですよね。
これはわかるのですが、
数式でハテナ?になるという馬鹿なんです…。
大体の人は屁理屈言っていると言われて会話は終了になるんです。
みたいに考えてました。
(考えてないですねこれじゃ笑)
⬆きちんと理解できるのが本当に羨ましいです。
優しくしてくださって本当にありがとうございます。+2
-0
-
82. 匿名 2017/04/04(火) 08:24:24
>>76
苦手な人はイメージできないのでは?
なので「こんな風にイメージしてみたら?」というのを図で表現したのだと思いますよ。+0
-0
-
83. 匿名 2017/04/04(火) 16:13:40
小学生の勉強くらいなら、子どもにも教えられる〜なんて、呑気なこと思ってた。
奥が深いね、難しいよ。+0
-0
-
84. 匿名 2017/04/04(火) 16:28:03
>>75
私もそう思います。
数Ⅲでも数字よりアルファベットの方が沢山出てくることも珍しくない。
数字の話話はどこいった?みたいな。
しかし、ピザの話や10の中に2はいくつある?を聞いて、目から鱗!
ますます、どう考えれば良いやらわからなくなってきました〜。+0
-0
-
85. 匿名 2017/04/04(火) 16:31:20
>>81
○㎞/h という「距離」を書くのか。
⬆一時間で何キロ進んだかの表記ですよね。
これはわかるのですが、
↑
でしたらゴールは目の前ですよ笑
「㎞/h」と「㎞ ÷ h」は、
「/ 」を「÷」に替えただけで
意味は同じです。
なので
速さ = ㎞/h
↓
速さ =「㎞(距離) ÷ h(時間)」
↓
速さ=距離÷時間
と、最初に書いてた式に辿り着きました笑
「1時間でたくさんの距離を進むには速く走るしか方法がない。
だから「速さ」なのに1時間で進んだ「距離(○㎞/h)」で表現するのだそうです。
まぁ許してやって下さい」
(ってお前誰だよ?笑)+1
-0
-
86. 匿名 2017/04/04(火) 16:58:16
>>84
私もそう思います。
ピザの話は目の前にある物を見て答えを求める「直感的タイプ」に対して、数学は答えを導くまでの「プロセス重視タイプ」なので直感的というわけにはいかない。
学校の算数数学は後者を教え後者の理解度で成績を決めるので、前者で理解する人には不利ですね。+0
-0
-
87. 匿名 2017/04/04(火) 17:34:36
こうやってバカがどんどん増えていく+0
-1
-
88. 匿名 2017/04/04(火) 17:37:54
>>83
かといって自分の知識だけで教えるのも危険なようですよ。![小学校3年生の算数問題が理解不能「21÷7は何の段の九九を使えば求まる?」答え 3の段←不正解]() 小学校3年生の算数問題が理解不能「21÷7は何の段の九九を使えば求まる?」答え 3の段←不正解girlschannel.net
小学校3年生の算数問題が理解不能「21÷7は何の段の九九を使えば求まる?」答え 3の段←不正解girlschannel.net小学校3年生の算数問題が理解不能「21÷7は何の段の九九を使えば求まる?」答え 3の段←不正解 最近の学校の教育が「大変なことになっている」と話題に|| ^^ |秒刊SUNDAY最近の小学校三年生の算数問題がなかなか理解不能だということで話題となっております。問題...
+0
-0
コメントを投稿する
トピック投稿後31日を過ぎると、コメント投稿ができなくなります。削除すべき不適切なコメントとして通報しますか?
いいえ
通報する


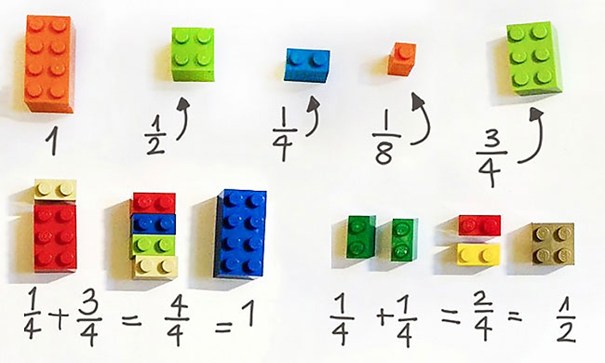












苦手な子どもが多い分数の計算。それを視覚的に理解しようと、浜松市内の小学生=当時=が「分数ものさし」を考えた。長さ12センチのものさしに5列の目盛りが付き、基準単位の「12分の1」がいくつあるか数えて計算する――。この発想に静岡大が注目し、教材化に向けた研究も進む。