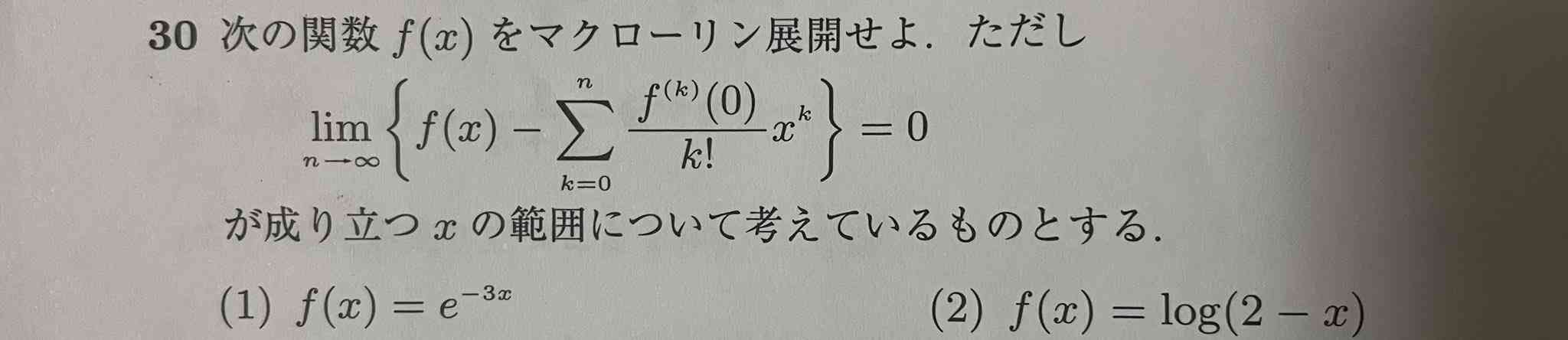【社会人の人】日々頭使いますか

[3. 匿名]

課題分からない
助けて

[56. 匿名]

>>3
あなた社会人？課題？

[60. 匿名]

>>3
知恵袋へGO

[62. 匿名]

>>3
ガチめに回答すると、
1. f(x) = e^(-3x) のマクローリン展開

まず、 f(x) = e^(-3x) を考える。

1.1 f(x) の各階微分
f(x) = e^(-3x)
f'(x) = -3e^(-3x)
f''(x) = 9e^(-3x)
f^(k)(x) = (-3)^k e^(-3x)
1.2 x = 0 における各階微分
f(0) = e^0 = 1
f'(0) = -3 * e^0 = -3
f''(0) = 9 * e^0 = 9
f^(k)(0) = (-3)^k
1.3 マクローリン展開式
f(x) = Σ[k=0~∞] (f^(k)(0) / k!) x^k = Σ[k=0~∞] ((-3)^k / k!) x^k

これは指数関数の展開式と同じ形：
e^(-3x) = Σ[k=0~∞] ((-3x)^k / k!)

したがって、マクローリン展開式は
e^(-3x) = Σ[k=0~∞] ((-3)^k / k!) x^k

2. f(x) = log(2 - x) のマクローリン展開

次に、 f(x) = log(2 - x) を考える

2.1 f(x) の各階微分
f(x) = log(2 - x)
f'(x) = -1 / (2 - x)
f''(x) = -1 / (2 - x)^2
f^(k)(x) = (-1)^(k+1) * (k-1)! / (2 - x)^k
2.2 x = 0 における各階微分
f(0) = log 2
f'(0) = -1 / 2
f''(0) = -1 / 4
f^(k)(0) = (-1)^(k+1) * (k-1)! / 2^k
2.3 マクローリン展開式
f(x) = Σ[k=0~∞] (f^(k)(0) / k!) x^k = log 2 + Σ[k=1~∞] ((-1)^(k+1) * (k-1)! / 2^k) / k! * x^k

ここで、(k-1)! / k! = 1 / k だから
f(x) = log 2 + Σ[k=1~∞] ((-1)^(k+1) / (k * 2^k)) x^k

これが f(x) = log(2 - x) のマクローリン展開式

範囲

マクローリン展開が収束する範囲を考えると、

[67. 匿名]

>>3
ネットで聞いた答え丸写しだと理屈理解しないから課題の意味ないじゃん

[70. 匿名]

>>3
発言小町へGo